Những tính chất tam giác vuông cân cần biết trong hình học

Tam giác vuông cân là một trong những loại tam giác đặc biệt mà các bạn học sinh sẽ được tìm hiểu trong chương trình toán hình 7. Vậy tam giác vuông cân có tính chất gì? Có các dạng bài tập nào liên quan đến tam giác vuông cân.

1. Nhắc lại khái niệm tam giác vuông cân

Tam giác vuông cân là tam giác vừa cân vừa vuông.

Bạn đang xem: Những tính chất tam giác vuông cân cần biết trong hình học

Tam giác vuông có hai cạnh bên bằng nhau thì là tam giác vuông cân.

Tam giác cân có 1 góc vuông thì tam giác đó là tam giác vuông cân

Ví dụ:

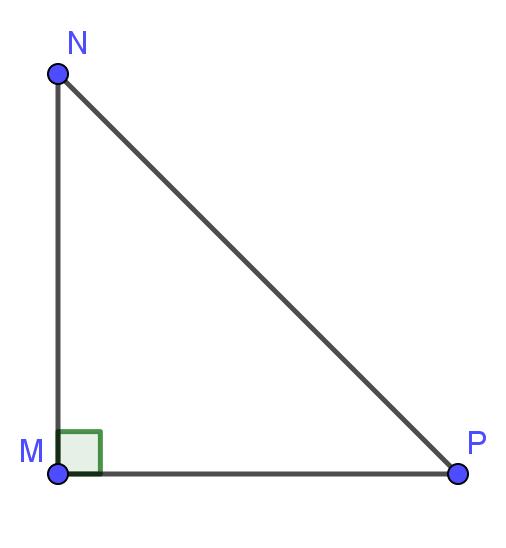
Tam giác MNP có một góc vuông là góc M và có hai cạnh MN = MP nên tam giác MNP là tam giác vuông cân tại M.

2. Các tính chất tam giác vuông cân

2.1. Tính chất 1

Tam giác vuông cân có hai góc ở đáy bằng nhau và bằng 45 độ

Ví dụ: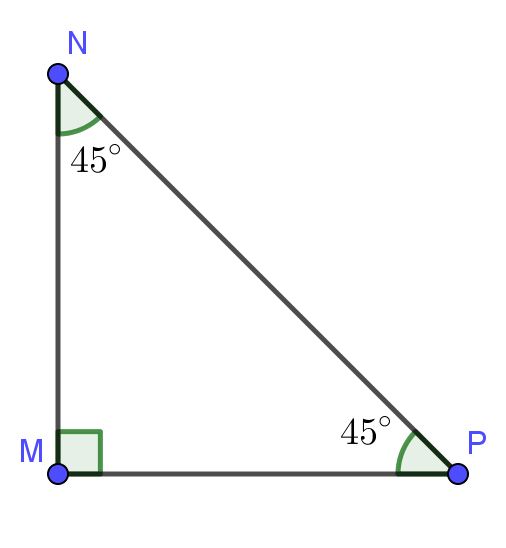

Tam giác MNP vuông cân tại M thì ta có:

2.2. Tính chất 2

Tam giác vuông cân có đường cao, đường phân giác, đường trung tuyến kẻ từ đỉnh của góc vuông trùng nhau và có độ dài bằng nửa cạnh huyền

Ví dụ: Tam giác MNP vuông cân tại M, đường trung tuyến, đường phân giác, đường cao kẻ từ M sẽ trùng nhau và bằng nửa cạnh NP

3. Dạng bài tập về tính chất tam giác vuông cân

3.1. Dạng 1: Dạng bài tập trắc nghiệm củng cố lý thuyết

Phương pháp giải: Dựa vào khái niệm, tính chất của tam giác vuông cân và các loại tam giác khác như tam giác đều, tam giác vuông, tam giác cân để chọn đáp án đúng nhất.

Bài tập luyện tập

Câu 1: Tam giác vuông cân là:

A. Tam giác có 1 góc vuông

B. Là tam giác có hai cạnh bằng nhau

C. Là tam giác có hai cạnh bên bằng nhau và một góc vuông

D. Là tam giác có ba cạnh bằng nhau

ĐÁP ÁN

Dựa vào khái niệm của tam giác vuông cân, ta chọn đáp án C

Câu 2: Hai góc ở đáy của tam giác vuông cân bằng

A. 90 độ

B. 45 độ

C. 60 độ

D. 50 độ

ĐÁP ÁN

Dựa vào tính chất 1 của tam giác vuông cân, ta chọn đáp án B

Câu 3: Cho tam MNP có MN = MP, góc M = 90 độ. Chọn đáp án đúng nhất

A. Tam giác MNP là tam giác vuông cân

B. Tam giác MNP là tam giác cân

C. Tam giác MNP là tam giác vuông

D. Tam giác MNP là tam giác đều

ĐÁP ÁN

Tam giác MNP có MN = MP nên tam giác MNP cân tại M

mà góc M = 90 độ nên tam giác MNP là tam giác vuông cân tại M

Vậy đáp án đúng là A

Câu 4: Cho tam giác MNP có góc MNP = 90 độ. Để tam giác MNP vuông cân thì

A. MP = MN

Xem thêm : Củ đậu rất tốt nhưng người mắc bệnh này không nên ăn

B. NP = NM

C. PM = PN

D. PM > PN

ĐÁP ÁN

Tam giác MNP có góc N = 90 độ nên tam giác MNP vuông tại N

Để tam giác MNP vuông cân thì NP = NM

Vậy đáp án đúng là B

Câu 5: Cho tam giác MNP có M = N = 45 độ. Chọn đáp án đúng nhất

A. tam giác MNP là tam giác cân

B. Tam giác MNP là tam giác đều

C. Tam giác MNP là tam giác vuông cân

D. Tam giác MNP là tam giác vuông

ĐÁP ÁN

Dựa vào tính chất 2 của tam giác vuông cân, ta chọn đáp án C

Câu 6: Chọn đáp án SAI:

A. Tam giác vuông là tam giác có một góc vuông

B. Tam giác đều là tam giác có hai cạnh bên bằng nhau và một góc bằng 90 độ

C. Tam giác vuông cân là tam giác có hai cạnh bên bằng nhau và một góc bằng 90 độ

D. Tam giác đều là tam giác có ba cạnh bằng nhau

ĐÁP ÁN

Đáp án B

3.2. Dạng 2: Dạng bài tập chứng minh

Phương pháp giải: Dựa vào tính chất tam giác vuông cân, tam giác đều, tam giác cân, tam giác vuông. Áp dụng linh hoạt các tính chất để giải quyết bài toán

Bài tập luyện tập

Bài 1: Cho tam giác MNP vuông cân tại M, kẻ đường cao MD của tam giác.

a) Chứng minh ND = DP = MD

b) Chứng minh tam giác MDP và MDN là tam giác vuông cân

ĐÁP ÁN

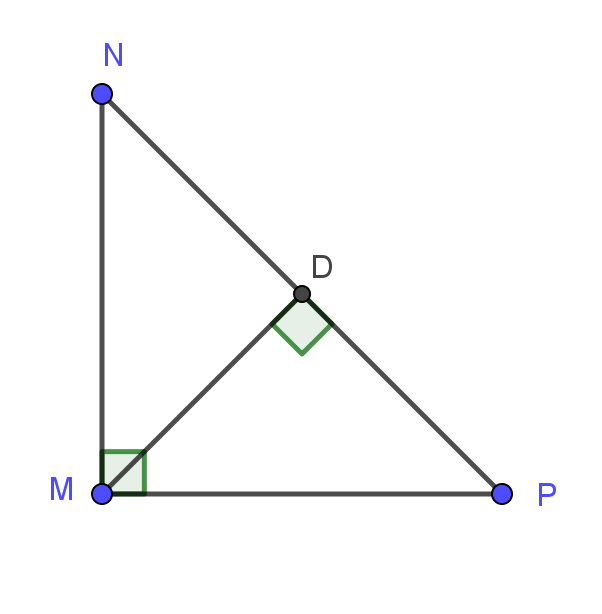
a) Vì tam giác MNP là tam giác vuông cân tại M nên theo tính chất 2 ta có:

MD = NP (1)

Tam giác MNP vuông cân tại M nên đường cao MD đồng thời cũng là đường trung tuyến, nên ND = DP = NP (2)

Từ (1) và (2) => ND = DP = MD

b) Theo tính chất 2, tam giác MNP vuông cân tại M nên đường cao MD đồng thời cũng là đường phân giác

=> (3)

Mà tam giác MNP vuông cân tại M nên : (4)

Từ (3), (4) =>

Xét tam giác DMP có:

=> tam giác DMP vuông cân tại D

Xét tam giác DMN có

Xem thêm : Hướng dẫn chi tiết cách hiện thước trong Word mới nhất

=> tam giác MDN vuông cân tại D

Bài 2: Cho tam giác MNP vuông cân tại M. Gọi A, B, D lần lượt là trung điểm của các cạnh MN, MP, NP.

a) Chứng minh AN = BP = AM = MB

b) Tam giác AMB là tam giác gì? Vì sao?

c) Chứng minh AB // NP

ĐÁP ÁN

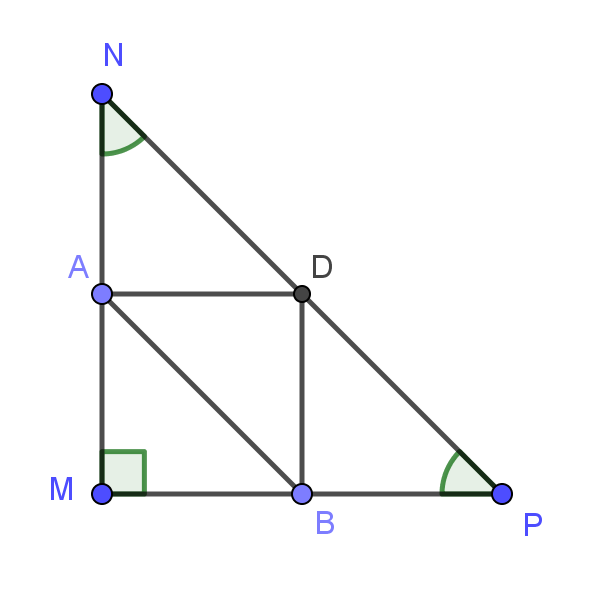
a) Ta có:

A là trung điểm của MN nên AN = AM = MN (1)

B là trung điểm của MP nên BP = MB = MP (2)

Mà tam giác MNP vuông cân tại M nên MP = MN (3)

Từ (1), (2), (3) => AN = BP= AM = MB

b) Theo phần a ta có: AM = MB => tam giác AMB cân tại M

Mà => tam giác AMB vuông cân tại M

c) Theo phần b, ta có: tam giác AMB vuông cân tại M

=> (4)

Mà tam giác MNP vuông cân tại M => (5)

Từ (4) và (5) =>

Mà hai góc này ở vị trí đồng vị => AB // NP

Bài 3: Cho tam giác NMP vuông cân tại M, trên cạnh NP lấy một điểm D bất kì. Từ D kẻ đường thắng vuông góc với MN cắt MN tại E.

a) Chứng minh rằng: DE // MP

b) Tam gác EDM và tam giác NED là tam giác gì? Vì sao?

ĐÁP ÁN

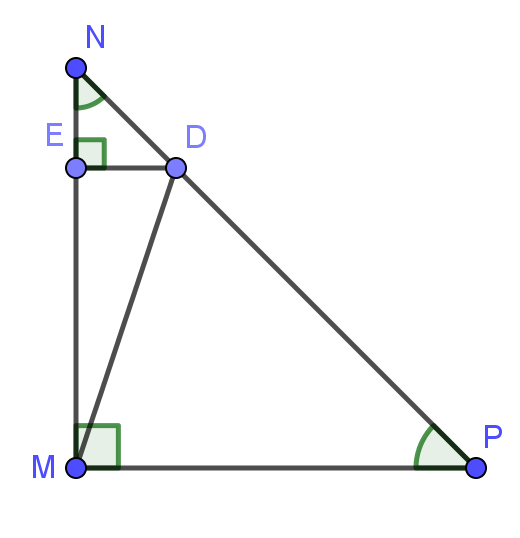
a) Ta có:

(theo đề bài)

(do tam giác MNP vuông cân tại M)

=> DE // MP (cùng vuông góc với MN)

b) Theo phần a, DE // MP

=> (SLT)

Mà (do tam giác MNP vuông cân tại M)

=>

Lại có: hay

Xét tam giác EDN có

Góc

=> tam giác NED là tam giác vuông cân tại E

* Tam giác MED có: ( )

=> MED là tam giác vuông tại E

Đây là toàn bộ phần lý thuyết về các tính chất tam giác vuông cân và một số bài tập liên quan. Hi vọng bài viết này sẽ giúp các bạn học sinh hiểu và áp dụng được để làm bài tập.

Chịu trách nhiệm nội dung: GV Nguyễn Thị Trang

Nguồn: https://duhochanquocchd.edu.vn
Danh mục: Khám Phá