Prime Numbers

Prime numbers are the numbers that have only two factors, that are, 1 and the number itself. Consider an example of number 5, which has only two factors 1 and 5. This means it is a prime number. Let us take another example of the number 6, which has more than two factors, i.e., 1, 2, 3, and 6. This means 6 is not a prime number. Now, if we take the example of the number 1, we know that it has only one factor. So, it cannot be a prime number as a prime number should have exactly two factors. This means 1 is neither a prime nor a composite number, it is a unique number.

Có thể bạn quan tâm

1. What are Prime Numbers? 2. Prime Numbers List 3. Properties of Prime Numbers 4. Prime and Composite Numbers 5. Prime and Co-prime Numbers 6. Easy Way to Find Prime Numbers 7. List of Odd Prime Numbers 8. FAQs on Prime Numbers

Bạn đang xem: Prime Numbers

A number greater than 1 with exactly two factors, i.e., 1 and the number itself is a prime number. For example, 7 has only 2 factors, 1 and 7 itself. So, it is a prime number. However, 6 has four factors, 1, 2, 3 and 6. Therefore, it is not a prime number. It is a composite number.

Prime Number Definition

Any whole number greater than 1 that is divisible only by 1 and itself, is defined as a prime number.

There are 25 prime numbers from 1 to 100. The complete list of prime numbers from 1 to 100 is given below:

Prime Numbers 1 to 100

List of Numbers Prime Numbers Between 1 and 10 2, 3, 5, 7 Between 11 and 20 11, 13, 17, 19 Between 21 and 30 23, 29 Between 31 and 40 31, 37 Between 41 and 50 41, 43, 47 Between 51 and 100

53, 59, 61, 67, 71, 73, 79, 83, 89, 97

☛ Check:

Check out a few more interesting articles related to prime numbers.

Natural Numbers
Prime Number Calculator
Prime Numbers Formula
Prime Factorization
Prime Numbers 1 to 1000
Prime Numbers 1 to 50
Prime Numbers 1 to 20
Prime Numbers 1 to 500
Prime Numbers 1 to 10
Prime Numbers Worksheets

Some of the important properties of prime numbers are given below:

A prime number is a whole number greater than 1.
It has exactly two factors, that is, 1 and the number itself.
There is only one even prime number, that is, 2.
Any two prime numbers are always co-prime to each other.
Every number can be expressed as the product of prime numbers.

A prime number is a number greater than 1 that has exactly two factors, while a composite number has more than two factors. For example, 5 can be factorized in only one way, that is, 1 × 5 (OR) 5 × 1. It has only two factors, which are, 1 and 5. Therefore, 5 is a prime number.
A composite number is a number greater than 1 that has more than two factors.For example, 4 can be factorized in multiple ways. So, the factors of 4 are 1, 2, and 4. It has more than two factors. Therefore, 4 is a composite number. Let us understand the difference between prime numbers and composite numbers with the help of the table given below:

Tham Khảo Thêm: Tuổi Mậu Dần 1998 mệnh gì? Hợp màu gì? Hợp tuổi nào? Công việc gì?

Prime Numbers Composite Numbers Numbers, greater than 1, having only two factors, 1 and the number itself Numbers greater than 1 having at least three factors 2 is the smallest and the only even prime number 4 is the smallest composite number Examples of prime numbers are 2, 3, 5, 7, 11, 13, and so on. Examples of composite numbers are 4, 6, 8, 9, 10, and so on.

There is a difference between prime numbers and co-prime numbers. The following points list the difference between prime and co-prime numbers.

Co-prime numbers are always considered in pairs, while a prime number is a single number.
If a pair of numbers has no common factor apart from 1, then the numbers are called co-prime numbers. Prime numbers do not have any such condition.
Co-prime numbers can be prime or composite, but the only condition is that the Greatest Common Factor (GCF) of co-prime numbers is always 1. Prime numbers are different from composite numbers because prime numbers are those numbers that have only 2 factors, 1 and the number itself.

Examples of Coprime Numbers

5 and 9 are co-primes. The factors of 5 are 1, 5; and the factors of 9 are 1, 3, and 9. We can see that they have only 1 as their common factor, therefore, they are coprime numbers.
6 and 11 are co-primes because they have only 1 as their common factor. The factors of 6 are 1, 2, 3 and 6; and the factors of 11 are 1 and 11. We can see that they have only 1 as their common factor, therefore, they are coprime numbers.
18 and 35 are co-primes because they have only 1 as their common factor. The factors of 18 are 1, 2, 3, 6, 9 and 18; and the factors of 35 are 1, 5, 7 and 35. We can see that they have only 1 as their common factor, therefore, they are coprime numbers.

It should be noted that Co-prime numbers need not necessarily be prime numbers.

Examples of Prime Numbers

A few examples of prime numbers are 2, 3, 5, 7, and so on.

There are different ways to find prime numbers. Let us go through one of these methods.

Method: Every prime number, apart from 2 and 3, can be written in the form of ‘6n + 1 or 6n – 1′. So, if we have any number different from 2 and 3, we can check if it is prime or not by trying to express it in the form of 6n + 1 or 6n – 1

Let us check this formula, 6n – 1, for the number 1, So, 6(1) – 1 = 5
Let us check this formula, 6n + 1 for the number 01, So, 6(1) + 1 = 7
Let us check this formula, 6n – 1, for the number 0, So, 6(2) – 1 = 11
Let us check this formula, 6n + 1, for the number 0, So, 6(2) + 1 = 13

Tham Khảo Thêm: 5 cách nạp thẻ Viettel cho thuê bao khác nhanh chóng

Now, we know that the numbers 5, 7, 11, and 13 are prime.

A prime number chart is a chart that shows the list of prime numbers in a systematic order. It should be noted that all prime numbers are odd numbers except for the number 2 which is an even number. Interestingly, 2 is the only prime number that is even. This means the list of odd numbers can start from 3 onwards and continue because the rest of the prime numbers are odd numbers. For example, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, and so on are odd prime numbers.

History of Prime Numbers

Xem thêm : Ngày tốt tháng 2 năm 2024 khai trương, cưới hỏi, làm nhà đại cát

Prime numbers have created human curiosity since ancient times. Even today, mathematicians are trying to find prime numbers with mystical properties. Euclid proposed the theorem on prime numbers – there are infinitely many prime numbers.

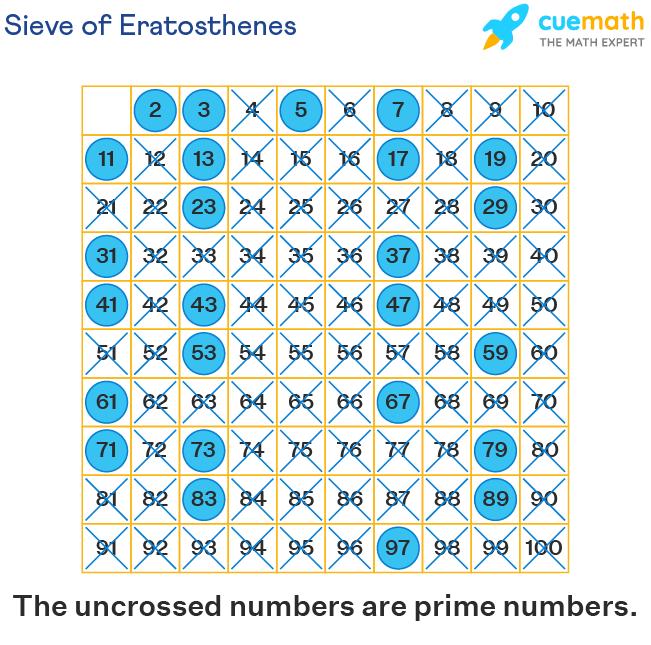
Do you know all the prime numbers from 1 to 100? Did you check if each number is divisible by the smaller numbers? Eratosthenes was one of the greatest scientists who lived a few decades after Euclid. He designed a smart way to determine all the prime numbers up to a given number. This method is called the Sieve of Eratosthenes. Let us learn about the Sieve of Eratosthenes in the following section.

Sieve of Eratosthenes

The Sieve of Eratosthenes is an ancient algorithm that helps to find prime numbers up to any given limit. The following figure shows the prime numbers up to 100 that are found using the Sieve of Eratosthenes. The uncrossed numbers in the figure represent the prime numbers that are left after using the Sieve of Eratosthenes.

Suppose we need to find the prime numbers up to ‘n’, so we will generate the list of all numbers from 2 to n. The following steps show how to find all the prime numbers up to 100 using the Sieve of Eratosthenes.

Step 1: First create a list of numbers from 2 to 100 as shown above. We leave the number 1 because all prime numbers are more than 1.
Step 2: We start from the first number 2 in the list. We cross out every number which is a multiple of 2 except 2. For example, we cross 4, 6, 8, 10, 12, 14, 16, and so on up to 100.
Step 3: Then, move on to the next unmarked (uncrossed) number which is 3. Cross out every number which is a multiple of 3 except 3. This will include a few multiples that are already crossed. So we cross the remaining ones. For example, 9, 15, 21, and so on up to 100.
Step 4: Then, we move to the next uncrossed number in the list after 3 which is 5. Cross out every number which is a multiple of 5 except 5. This will include a few multiples that are already crossed. So we cross the remaining ones. For example, 25, 35, 55, and so on up to 100.
Step 5: 7 is the next uncrossed number in the list after 5. So, cross out every number which is a multiple of 7 except 7. This will include a few multiples that are already crossed. So we cross the remaining ones. For example, 49. After this step, we will be left with only prime numbers. In other words, the Sieve of Eratosthenes filters out all numbers and only prime numbers are left behind. Observe the numbers that are crossed and that are left as prime numbers in the Sieve of Eratosthenes given above.

Tham Khảo Thêm: Cách sử dụng hạt chia giảm cân một cách hiệu quả và giảm mỡ bụng nhanh chóng

Smallest Prime Number

The smallest prime number is 2. Interestingly, this is the only even number that is a prime number. It should be noted that 1 is neither a prime number nor a composite number because it has only 1 factor which is 1, hence, it is a unique number.

Even Prime Number

The only prime number which is an even number is 2. This means all even numbers are composite numbers. 2 is a prime number because it has only 2 factors 1 and the number 2 itself.

Largest Prime Number

The largest prime number cannot be listed because numbers are infinite and the largest prime number cannot be determined.

Important Tips on Prime Numbers

The only even prime number is 2.
The first five prime numbers are 2, 3, 5, 7, and 11.
All prime numbers are not odd. This is because 2 is an even number and a prime number as well. In fact, 2 is the only even prime number.
1 is neither a prime number nor a composite number.

☛ Topics Related to Prime Numbers

Is 1 a Prime Number?

Is 2 a Prime Number?

Is 5 a Prime Number?

Is 7 a Prime Number?

Is 9 a Prime Number?

Is 11 a Prime Number?

Is 13 a Prime Number?

Is 17 a Prime Number?

Is 19 a Prime Number?

Is 23 a Prime Number?

Xem thêm : Sữa cho mẹ bầu